Resolution #
Resolution is defined as the distance between two adjacent peak apexes, divided by the average base width of both peaks. It is represented by the equation:
$ R = \frac{(T_2 - T_1)}{0.5(W_1 + W_2)} $
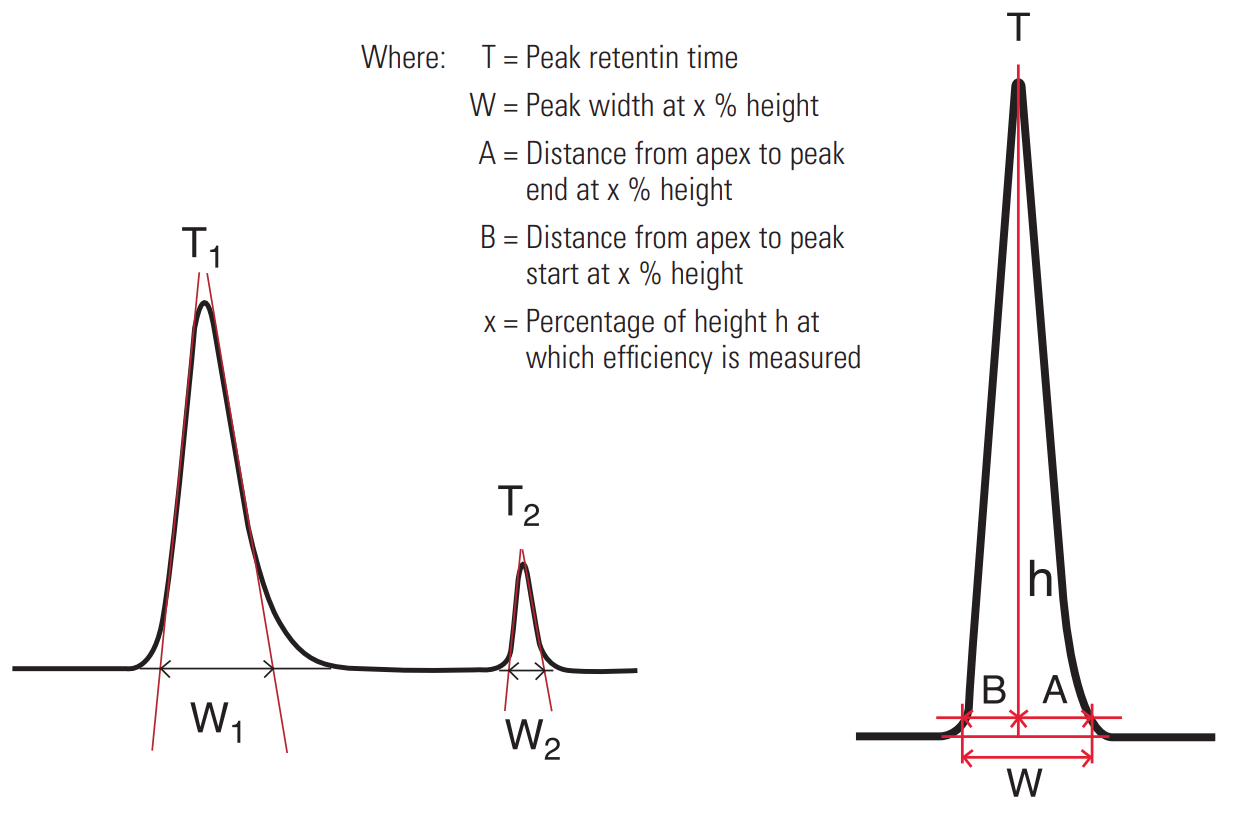
Resolution is dependant on three other variables, the column efficiency N, the capacity factor k’ and the selectivity α.
Decreasing N decreases the resolution because peak width increases. Increasing N increases resolution because peak width decreases.
Decreasing k’ sharpens the peaks but decreases resolution. Increasing k’ broadens the peaks but improves resolution.
Increasing α increases resolution. One peak moves relative to the other. Likewise, decreasing α decreases resolution.
Column Efficiency (N) #
Column efficiency, or the theoretical plate count, is a measure of peak band spreading. The lower the level of band spreading, the higher the column efficiency and vice versa.
Important: The column efficiency figure quoted on the supplied certificate of analysis is actually the efficiency for the column AND HPLC system. If the efficiency calculation is repeated on a different instrument when the column is new, it is very likely that there will be a difference between the certificated value of N and your new calculated value of N. This difference is not due to the column but the instrument.

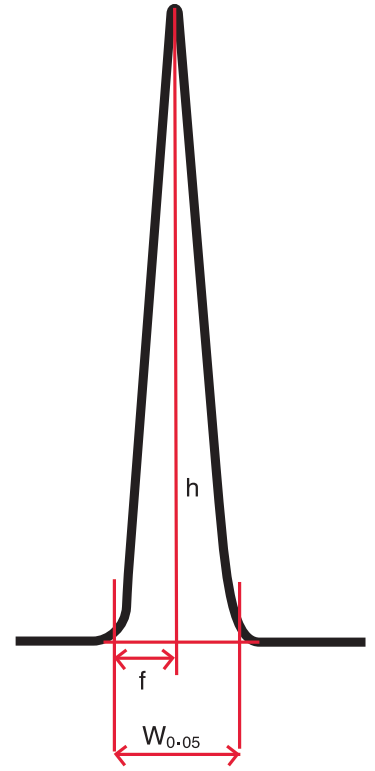
Tailing Factor (T) #
Tailing factor is a measure of the symmetry of a peak. A peak’s tailing factor is measured using the following equation:
$T = \frac{W_{0.05}}{2f}$
Where $ W_{0.05} = $ peak width at 5% height
f = distance from peak front to apex point at the baseline
Capacity Factor (k) #
Capacity factor is a measure of the retention of an analyte relative to the column void volume, $V_0$. It is measured using the following equation:
$ k = \frac{V_1 - V_0}{V_0} $
Where $V_0 =$ Column void volume
$V_1 =$ Retention volume of peak
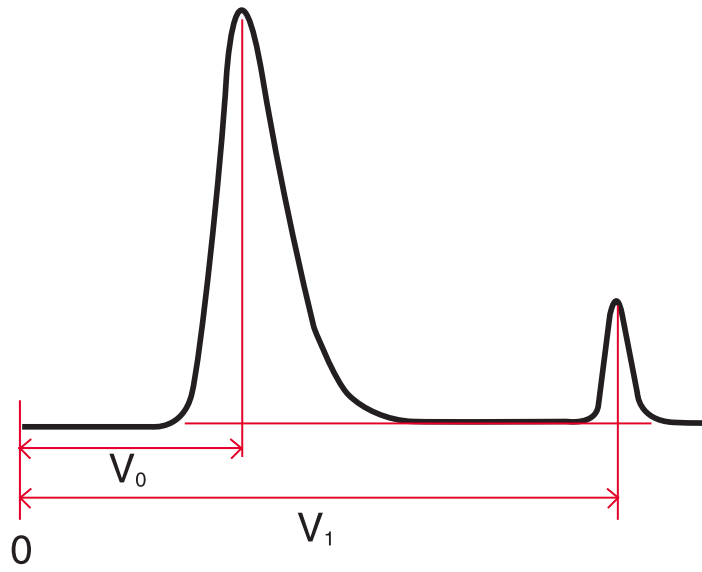
Important: The column void volume can be measured by injecting a compound that will be unretained by the column packing. Typical compounds used include uracil (RP) and toluene (NP).
Changes in capacity factor that occur both with standard and sample mixes are likely to be due to changes in the column, temperature or mobile phase composition.
Changes in capacity factor that occur only in the sample mix and not the standard mix are most likely to be due to the composition of the sample.
Capacity factor is affected by changes in mobile phase, operating temperature, analyte retention characteristics and changes to the surface chemistry of the column.
Note: Capacity factor will change by up to 10% for a 5 °C rise in column temperature.
Selectivity ($\alpha$) #
Selectivity is a measure of the relative retention of two adjacent peaks in a chromatogram. It can be calculated using capacity factors or retention volumes:
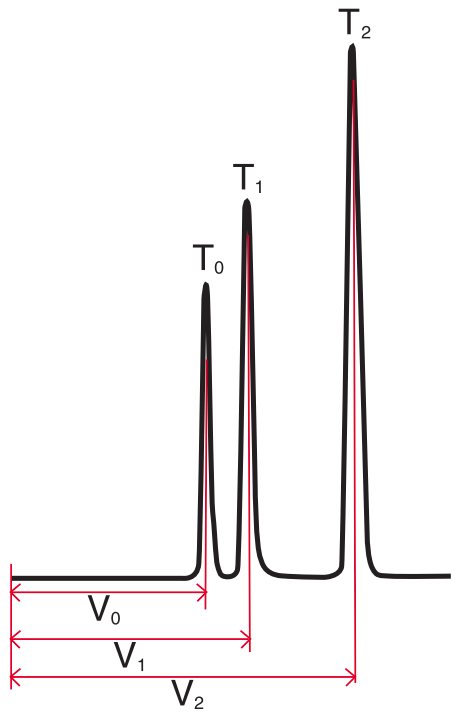
$ \alpha = \frac{k_2}{k_1} = \frac{V_2 - V_0}{V_1 - V_0} $
Where $K_1 = V_1$ capacity factor
$K_2 = V_2$ capacity factor
$V_0 =$ void volume
$V_1 =$ peak 1 retention time
$V_2 =$ peak 2 retention time
Selectivity can be affected by changes in mobile phase composition, temperature and column chemistry.
Changes in selectivity that occur both with standard and sample mixes are most likely to be due to changes in the column, temperature or mobile phase composition.
Changes in selectivity that occur only in the sample mix and not the standard mix are most likely to be due to the composition of the sample.